Published in Blog
Generate the optimal soccer schedule with Timefold
Learn how to code an automated tournament scheduling service with Timefold Solver
If you’ve ever organized a tournament with many teams, you know how hard it is to generate a good and fair tournament schedule that complies with all the rules, regardless if it’s for the national soccer league or your local padel competition.
In this article, we describe how we can create a tournament schedule and adapt it to your needs using Timefold Solver. The tournament we create is similar to a national soccer league: a fixed number of teams, each facing every other team two times.
We use Timefold Solver, which is the open-source AI solver to optimize operations and scheduling in Java, Python or Kotlin. Let’s delve deeper into the problem!
The rules of the tournament schedule
Our league consists of a variable number of teams and a variable number of rounds, with the following rules:
-
Each team has to face every other team twice, one time playing at home, the other time playing away.
-
All teams should play once per round; if the number of teams is odd, one team will not play per round.
-
The league should consist of two parts with equal rounds, with the teams switching the home stadium (eg. if the tournament has 4 rounds, round 1 and round 3 will have the same teams facing each other but the away team switching to be the home team, and vice-versa).
-
Rival teams should not face in the first round.
-
It should be prevented that the teams play many consecutive games home or away.
Let’s see how we can model that in Java with Timefold Solver.
Implementation with Timefold Solver
To create the tournament schedule, we use Java with Quarkus. The implementation is available in this GitHub repo.
The central domain object of the problem is the team. We schedule matches that have two teams: a home team and an away team. Each match also belongs to a specific round. We also want to know the rivalries between the teams, so that we avoid having matches between rivals in the first round.
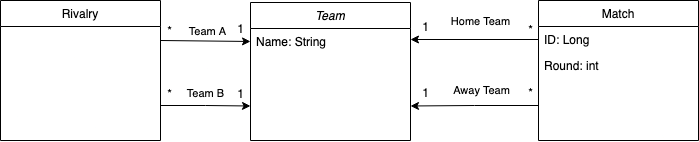
But how do we use Timefold Solver to create our schedule?
We only schedule half of the tournament, since the other half merely mirrors the rounds with the home/away teams swapped. This simplifies our scheduling problem.
Let’s suppose that we are only given the team names that are going to play in this tournament. We already know in advance the number of rounds and games per round that exist, so those are problem facts, as they don’t change during the scheduling.
|
Note
|
If the number of teams is even, the number of rounds is the number of teams minus one and the number of games per round is half of the number of teams. If the number of teams is odd, the number of rounds is the number of teams and the number of games per round is half of the number of teams minus one. |
What changes during the scheduling is the teams that play in each match. So the match has the @PlanningEntity annotation and the home team and the away team have the @PlanningVariable annotation. The solver changes the @PlanningVariables in the @PlanningEntity annotated objects to optimize the solution. More information about problem facts and planning entities can be seen in the docs.
@PlanningEntity
public class Match {
@PlanningId
private Long id;
@PlanningVariable
private Team homeTeam;
@PlanningVariable
private Team awayTeam;
private int round;
public Match() {
}
public Match(Long id, int round) {
this.id = id;
this.round = round;
}
public Long getId() {
return id;
}
public Team getHomeTeam() {
return homeTeam;
}
public Team getAwayTeam() {
return awayTeam;
}
public int getRound() {
return round;
}
}We also need a class that is our @PlanningSolution, with the problem facts for the problem. Let’s call it TournamentSchedule.
This object has a list of teams from which the solver can choose to populate the schedule. That is indicated by the annotation @ValueRangeProvider.
It is also needed to annotate with @ProblemFactCollectionProperty the problem facts to be used by the constraints, as well as the list of matches to optimize, with @PlanningEntityCollectionProperty.
@PlanningSolution
public class TournamentSchedule {
@PlanningEntityCollectionProperty
private List<Match> matches;
@ValueRangeProvider
@ProblemFactCollectionProperty
private List<Team> teams;
@ProblemFactCollectionProperty
private List<Rivalry> rivalries;
@PlanningScore
private HardSoftScore score;
public TournamentSchedule() {
}
public TournamentSchedule(List<Team> teams, List<Rivalry> rivalries) {
this.matches = generateMatches(teams);
this.teams = teams;
this.rivalries = rivalries;
}
private List<Match> generateMatches(List<Team> teams) {
int numberOfRounds = (teams.size() % 2 == 0) ? teams.size() - 1 : teams.size();
int gamesPerRound = teams.size() / 2;
List<Match> matches = new ArrayList<>();
int id = 0;
for(int round: IntStream.range(0, numberOfRounds).boxed().toList()) {
for(int game: IntStream.range(0, gamesPerRound).boxed().toList()) {
matches.add(new Match((long) id++, round));
}
}
return matches;
}
public List<Match> getMatches() {
return matches;
}
public List<Rivalry> getRivalries() {
return rivalries;
}
public HardSoftScore getScore() {
return score;
}
@Override
public String toString() {
StringBuilder result = new StringBuilder();
matches.stream().collect(Collectors.groupingBy(Match::getRound))
.forEach((round, matches) -> {
result.append("Round ").append(round).append(": \n");
String roundMatchesString = matches.stream()
.map(match -> "\t" + match.getHomeTeam().getName() + " vs " + match.getAwayTeam().getName())
.collect(Collectors.joining("\n"));
result.append(roundMatchesString).append("\n\n");
});
return result.toString();
}
}Now that our entities are set up, let’s create an empty list of constraints.
public class ScheduleConstraintProvider implements ConstraintProvider {
@Override
public Constraint[] defineConstraints(ConstraintFactory constraintFactory) {
return new Constraint[] {};
}
}Finally, let’s create an endpoint, and create four teams with two rivalries, so that we can run the solver!
@Path("/solve")
public class SolverResource {
@Inject
SolverManager<TournamentSchedule, UUID> solverManager;
@GET
public String solve() {
UUID problemId = UUID.randomUUID();
List<Team> teams = List.of(
new Team("A"),
new Team("B"),
new Team("C"),
new Team("D")
);
List<Rivalry> rivalries = List.of(
new Rivalry(teams.get(0), teams.get(1)),
new Rivalry(teams.get(0), teams.get(2))
);
TournamentSchedule problem = new TournamentSchedule(teams, rivalries);
// Submit the problem to start solving
SolverJob<TournamentSchedule, UUID> solverJob = solverManager.solve(problemId, problem);
TournamentSchedule solution;
try {
// Wait until the solving ends
solution = solverJob.getFinalBestSolution();
} catch (InterruptedException | ExecutionException e) {
throw new IllegalStateException("Solving failed.", e);
}
return solution.toString();
}
}Start the application and try it out!
> mvn quarkus:dev❯ curl localhost:8080/solve
Round 0:
A vs A
A vs A
Round 1:
A vs A
A vs A
Round 2:
A vs A
A vs AIt seems that the first team is chosen to play in all rounds! That happened because we do not have any constraints yet. There is nothing to tell the solver which situations it should prefer or avoid. Let’s add them!
Constraints
Let’s start with the basic constraints and see where our schedule looks funny. The first thing we don’t want is that a team is scheduled to play against itself.
In Timefold Solver, we can configure hard and soft constraints. A hard constraint cannot be broken, and breaking a hard constraint would mean that the solution is not acceptable. Soft constraints can be broken but that should be avoided. Since a team playing against itself is impossible, let’s configure it as a hard constraint. More information about constraints and score is available in the docs.
@Override
public Constraint[] defineConstraints(ConstraintFactory constraintFactory) {
return new Constraint[] {
teamCannotPlayAgainstItself(constraintFactory),
};
}
private Constraint teamCannotPlayAgainstItself(ConstraintFactory constraintFactory) {
return constraintFactory
.forEach(Match.class)
.filter(match -> match.getHomeTeam() == match.getAwayTeam())
.penalize(HardSoftScore.ONE_HARD)
.asConstraint("A team cannot play against itself");
}❯ curl localhost:8080/solve
Round 0:
B vs A
B vs A
Round 1:
B vs A
B vs A
Round 2:
B vs A
B vs AGreat! By running the solver, we see that now no team is facing itself, but there are always the same two teams facing each other. Let’s add a hard constraint so each two teams can only face once (Rule 1).
@Override
public Constraint[] defineConstraints(ConstraintFactory constraintFactory) {
return new Constraint[] {
teamCannotPlayAgainstItself(constraintFactory),
twoTeamsCanOnlyFaceOneTime(constraintFactory)
};
}
//...
private Constraint twoTeamsCanOnlyFaceOneTime(ConstraintFactory constraintFactory) {
return constraintFactory
.forEachUniquePair(Match.class)
.filter((match1, match2) -> (match1.getHomeTeam() == match2.getHomeTeam() &&
match1.getAwayTeam() == match2.getAwayTeam()) ||
(match1.getHomeTeam() == match2.getAwayTeam() &&
match1.getAwayTeam() == match2.getHomeTeam())
)
.penalize(HardSoftScore.ONE_HARD)
.asConstraint("Two teams can only face each other one time");
}❯ curl localhost:8080/solve
Round 0:
B vs A
C vs A
Round 1:
D vs A
C vs B
Round 2:
D vs B
D vs CNow teams are only facing each other once, but are still playing more than once per round (see the A team in the first round) (Rule 2). Let’s add another hard constraint to solve that.
@Override
public Constraint[] defineConstraints(ConstraintFactory constraintFactory) {
return new Constraint[] {
teamCannotPlayAgainstItself(constraintFactory),
twoTeamsCanOnlyFaceOneTime(constraintFactory),
teamOnlyOnceInRound(constraintFactory)
};
}
// ...
private Constraint teamOnlyOnceInRound(ConstraintFactory constraintFactory) {
return constraintFactory
.forEachUniquePair(Match.class, equal(Match::getRound))
.filter((match1, match2) -> match1.getHomeTeam() == match2.getHomeTeam()
|| match1.getAwayTeam() == match2.getHomeTeam()
|| match1.getHomeTeam() == match2.getAwayTeam()
|| match1.getAwayTeam() == match2.getAwayTeam()
)
.penalize(HardSoftScore.ONE_HARD)
.asConstraint("Each team can only play once per round");
}❯ curl localhost:8080/solve
Round 0:
B vs A
D vs C
Round 1:
C vs A
D vs B
Round 2:
D vs A
C vs BWow, now the schedule is starting to look much more feasible. No more physical impossibilities neither impossible rounds. We are just breaking two more rules. Teams are playing too many consecutive games at home or away (Rule 5). For example, team D is always playing at home. Let’s implement a soft constraint to avoid that.
@Override
public Constraint[] defineConstraints(ConstraintFactory constraintFactory) {
return new Constraint[] {
teamCannotPlayAgainstItself(constraintFactory),
twoTeamsCanOnlyFaceOneTime(constraintFactory),
teamOnlyOnceInRound(constraintFactory),
// Soft constraints
eachTeamShouldNotPlayManyConsecutiveGamesAtHomeOrAway(constraintFactory)
};
}
// ...
private Constraint eachTeamShouldNotPlayManyConsecutiveGamesAtHomeOrAway(ConstraintFactory constraintFactory) {
return constraintFactory
.forEachUniquePair(Match.class)
.filter(
(match1, match2) -> (match1.getRound() == match2.getRound() + 1 &&
(match1.getHomeTeam() == match2.getHomeTeam() || match1.getAwayTeam() == match2.getAwayTeam())) ||
(match1.getRound() + 1 == match2.getRound() &&
(match1.getHomeTeam() == match2.getHomeTeam() || match1.getAwayTeam() == match2.getAwayTeam()))
)
.penalize(HardSoftScore.ONE_SOFT)
.asConstraint("A team should not play two consecutive house or away games");
}❯ curl localhost:8080/solve
Round 0:
B vs A
D vs C
Round 1:
C vs B
A vs D
Round 2:
C vs A
D vs BWe can see that sometimes it’s impossible for all teams to not play two consecutive away and home matches (for example, D is playing rounds 1 and 2 away), but we can limit that to at most once per team. Finally, the rival teams are A with B and A with C. So we would like to start the schedule with the game A vs D. Let’s implement another soft constraint to avoid rival teams facing each other in the first round (Rule 4).
@Override
public Constraint[] defineConstraints(ConstraintFactory constraintFactory) {
return new Constraint[] {
teamCannotPlayAgainstItself(constraintFactory),
twoTeamsCanOnlyFaceOneTime(constraintFactory),
teamOnlyOnceInRound(constraintFactory),
// Soft constraints
eachTeamShouldNotPlayManyConsecutiveGamesAtHomeOrAway(constraintFactory),
rivalTeamsShouldNotFaceOnFirstRound(constraintFactory)
};
}
// ...
private Constraint rivalTeamsShouldNotFaceOnFirstRound(ConstraintFactory constraintFactory) {
return constraintFactory
.forEach(Match.class)
.filter(match -> match.getRound() == 0)
.join(Rivalry.class)
.filter((match, rivalry) ->
(match.getHomeTeam() == rivalry.getTeamA() && match.getAwayTeam() == rivalry.getTeamB()) ||
(match.getHomeTeam() == rivalry.getTeamB() && match.getAwayTeam() == rivalry.getTeamA())
)
.penalize(HardSoftScore.ONE_SOFT)
.asConstraint("Rival teams should not face on first round");
}❯ curl localhost:8080/solve
Round 0:
D vs A
C vs B
Round 1:
A vs C
B vs D
Round 2:
B vs A
D vs CTournament schedule with 20 teams
Now we have a full tournament scheduling algorithm according to the rules. The best part is that now it is possible to create a tournament with as many teams as we want to. For example, you can see the full scheduling for 20 teams and no rivalries below.
Tournament Scheduling for 20 teams
❯ curl localhost:8080/solve
Round 0:
N vs K
L vs C
R vs D
S vs B
J vs I
E vs Q
H vs T
F vs A
G vs O
P vs M
Round 1:
L vs H
S vs Q
O vs M
A vs C
J vs E
I vs T
G vs F
C vs R
N vs P
D vs K
Round 2:
S vs D
A vs J
L vs E
H vs P
G vs B
N vs C
L vs T
F vs O
I vs Q
R vs M
Round 3:
I vs S
E vs D
N vs G
B vs C
J vs H
O vs A
M vs Q
F vs K
R vs T
P vs L
Round 4:
T vs F
H vs Q
I vs L
C vs K
E vs M
J vs N
D vs O
I vs B
S vs P
G vs R
Round 5:
E vs T
F vs D
Q vs B
G vs S
A vs P
I vs N
B vs R
L vs K
C vs H
O vs J
Round 6:
Q vs K
D vs I
S vs N
M vs R
G vs L
P vs B
H vs O
E vs F
N vs T
C vs J
Round 7:
G vs E
I vs K
O vs O
C vs F
B vs H
R vs N
S vs A
J vs P
T vs D
M vs L
Round 8:
K vs S
L vs R
I vs G
H vs F
M vs B
J vs T
A vs Q
E vs P
M vs N
D vs C
Round 9:
K vs H
S vs L
M vs J
G vs D
T vs C
I vs I
P vs O
B vs E
A vs H
R vs Q
Round 10:
P vs R
I vs O
D vs A
L vs N
M vs S
F vs J
H vs G
E vs K
T vs B
C vs Q
Round 11:
N vs S
T vs M
R vs I
A vs L
J vs D
P vs F
H vs H
O vs K
E vs S
G vs Q
Round 12:
C vs R
N vs H
M vs G
K vs T
J vs B
I vs F
L vs D
P vs Q
A vs E
O vs S
Round 13:
E vs C
I vs A
R vs O
D vs Q
K vs B
S vs T
G vs P
F vs N
H vs M
L vs J
Round 14:
I vs P
E vs N
H vs R
K vs K
T vs O
C vs G
J vs S
Q vs L
A vs B
M vs D
Round 15:
C vs P
O vs Q
T vs L
K vs M
C vs I
G vs A
B vs N
J vs R
E vs H
S vs F
Round 16:
I vs M
L vs B
O vs C
Q vs F
P vs T
A vs K
H vs D
O vs N
R vs S
G vs E
Round 17:
F vs L
K vs J
T vs Q
T vs G
R vs A
P vs D
S vs H
C vs M
O vs B
E vs I
Round 18:
A vs T
N vs Q
C vs S
E vs R
L vs O
F vs M
J vs G
B vs D
K vs P
I vs HWe suggest you to add your own rules to try the solver, such as:
-
Add a list of referees to the problem and try to attribute them to each match fairly: each of them should have a similar number of matches, with no more than one match per round, and a similar number of matches between the teams.
-
Schedule the matches between closer teams to earlier in the tournament.
-
Take into account the time and schedule the matches between rivals to the peak hours with no match overlapping another.
Share your experiments with the community. We can’t wait to know what you build!